강의노트 z-변환

개요

표본기는 T초 마다 닫히는 스위치이다.

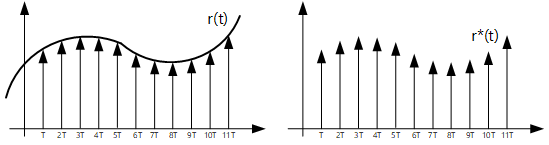
입력된 연속 신호를 r(t)를 표본기를 지나면 r*(t)의 이산신호가 된다.

nT시간의 이산값은 식(1)과 같다.

$$\tag{1} r^{*} (nT) = r(nT) \delta (t-nT)$$

모든 신호 r(t)에 대한 이산 신호는

$$\tag{2} r^{*}(t) = \sum_{k=0}^{\infty} r(kT) \delta(t-kT) = r(0)\delta(t) + r(T)\delta(t-T) + r(2T) \delta(t-2T)+...$$

$r^{ * }(kT)$에 대한 라플라스 변환은 $\mathcal{L} [r^{ * }(kT)] = F^{ * }(s)$이고 식(3)과 같다.

$$\tag{3} F^{ * }(s) = \mathcal{L} [r^{ * }(t)]= \mathcal{L} \left[ \sum_{k=0}^{\infty} r(kT) \delta(t-kT) \right] = \sum_{k=0}^{\infty} r(kT) e^{-ksT} \xrightarrow{z = e^{sT}} \sum_{k=0}^{\infty} r(kT) z^{-k}= Z[r^{ * }(t)] = R(z)$$

식(3)은 r(t)신호의 이산 신호에 대한 라플라스 변환을 진행한 것으로 볼 수 있으며 이를 r(t)의 z-변환이라 한다.

위의 과정을 통해 z-변환은 :

1. f(t)의 샘플링으로 f(kT)을 얻는다. f(kT)는 임펄스 함수들의 열의 집합이다.
2. 임펄스 열의 라플라스 변환($F^{ * }(s)$)을 취한다. $F^{ * }(s)$는 $e^{sT}$항을 포함하고 있다.
3. $z = e^{sT}$ 치환하면 $F^{ * }(s) = F(z)$가 된다.

주의 : f(t)의 라플라스 변환 값 $\mathcal{L}(f(t)) = F(s)$는 $F(z)$와 같지 않다. 즉, $F(s) \ne F(z)$

z-변환 예제

단위 계단 함수의 z-변환

u(t)함수를 이산 신호로 만들면 식(4)와 같다.

$$\tag{4} u(t) = \sum_{k=0}^{\infty} u(kT) \delta(t-kT)$$

$$\tag{5} U(z) = Z[u(t)] = \sum_{k=0}^{\infty} u(kT) z^{-k} \xrightarrow{u(kT) = 1} \sum_{k=0}^{\infty} z^{-k} = \dfrac{1}{1-z^{-1}}=\dfrac{z}{z-1}$$

지수함수의 z-변환

$$r(t) = e^{-at} \xrightarrow {discretization} r^{ * }(kT) = e^{-akT} \quad, \quad t \geqslant 0$$

z-변환하면

$$\tag{6} R(z) = Z[r^{ * }(kT)] = Z[e^{-akT}]= \sum_{k=0}^{\infty} r(kT) z^{-k} = \sum_{k=0}^{\infty} e^{-akT} z^{-k} = \sum_{k=0}^{\infty} (ze^{aT})^{-k} = \dfrac{1}{1 - (ze^{aT})^{-1}} = \dfrac{z}{z-e^{-aT}}$$

sin함수의 z-변환

$$\tag{7} r(t) = \sin (\omega t) \xrightarrow{discretization} r^{ * }(kT) = \sin (\omega kT)\quad, \quad t \geqslant 0$$

오일러 공식을 이용하여 식(7)을 식(8)과 같이 변형한다.

$$\tag{8} \sin (\omega t) = \dfrac{e^{j \omega t} - e^{-j \omega t } }{2j}$$

식(8)을 식(7)에 대입하면

$$r^{ * }(kT) = \sin (\omega kT) = \dfrac{e^{j \omega kT} - e^{-j \omega kT } }{2j}$$

z-변환하면

$$\tag{9} R(z) = Z[r^{ * }(kT)] = Z[\sin (\omega kT)]= \sum_{k=0}^{\infty} r(kT) z^{-k} = \sum_{k=0}^{\infty} \dfrac{e^{j \omega t} - e^{-j \omega t } }{2j} z^{-k} = \dfrac{1}{2j} \left( Z[e^{j \omega t}]-Z[ e^{-j \omega t }] \right) = \dfrac{1}{2j} \left( \dfrac{z}{z - e^{j \omega T}} -\dfrac{z}{z - e^{-j \omega T}} \right)$$

$$\tag{10} R(z) = Z[\sin (\omega t)] = \dfrac{1}{2j}\dfrac{z(z - e^{-j \omega T})-z(z - e^{j \omega T})}{(z - e^{j \omega T})(z - e^{-j \omega T})} = \dfrac{1}{2j} \dfrac{z(e^{j \omega T}- e^{-j \omega T})}{z^2 -(e^{j \omega T}+ e^{-j \omega T})z +1} = \dfrac{z \sin (\omega T)}{z^2 -2 \cos (\omega T) +1}$$

램프함수에 대한 z-변환

$$f(t) = t, \quad t \ge 0 \xrightarrow{discretization} f(t)= \sum_{k=0}^{\infty} (kT)\delta(t-kT)$$

z-변환을

$$\tag{11} F(z) = \sum_{k = 1}^{\infty} (kT)z^{-k} = \dfrac{T}{z}+\dfrac{2T}{z^2}+\dfrac{3T}{z^3}+...$$

식(11)을 zT로 나누면 식(12)와 같아진다.

$$\tag{12} \dfrac{F(z)}{zT} = \dfrac{1}{z^2}+\dfrac{2}{z^3}+\dfrac{3}{z^4}+...$$

식(12)에 적분을 취하면

$$\tag{13} \int{\dfrac{F(z)}{zT}}dz = -\dfrac{1}{z}-\dfrac{1}{z^2}-\dfrac{1}{z^3}-...+\alpha$$

여기서, $\alpha$는 적분 상수이다.

식(13)의 오른쪽 항은 무한 등비수열이고 이 합은 식(14)가 된다.

$$\tag{14} \int{\dfrac{F(z)}{zT}}dz = -\dfrac{1}{z-1}+\alpha$$

식(14)에 미분을 취하면

$$\tag{15} \dfrac{F(z)}{zT} = \dfrac{1}{(z-1)^2}$$

그러므로,

$$\tag{16} F(z) = \dfrac{zT}{(z-1)^2}$$

수열 $a^k$에 대한 z-변환

$$f(t) = \sum_{k=0}^{\infty} a^k \xrightarrow{discretization} f(kT) = \sum_{k=0}^{\infty} a^k \delta(t-kT)$$

$$F(z) = \sum_{k=0}^{\infty} a^k z^{-k} = 1 + \dfrac{a}{z}+ \dfrac{a^2}{z^2}+ \dfrac{a^3}{z^3} + ...$$

이는 첫항이 1이고 등비가 $\dfrac{a}{z}$인 무한 등비수열이고 이 합은

$$F(z) = \dfrac{1}{1- a/z} = \dfrac{z}{z-a}$$

라플라스 함수에 대한 z-변환

$X(s) = \mathcal{L}[x(t)] = \dfrac{1}{s(s+1)}$에 대한 z-변환을 구한다.

$$X(z) = Z[x(t)]=Z \left[ \mathcal{L}^{-1} \left( \dfrac{1}{s(s+1)} \right) \right]= Z \left[ \mathcal{L}^{-1} \left( \dfrac{1}{s} - \dfrac{1}{s+1} \right) \right]=Z [u(t) - e^{-t}]= Z[u(t)] - Z[e^{-t}]$$

$$X(z) = \dfrac{z}{z-1} - \dfrac{z}{z-e^{-T}} = \dfrac{z(1-e^{-T})}{(z-1)(z-e^{-T})}$$