정리와 속성
f(t)함수의 이산화된 값은 f∗(kT)=∑k=0∞f(kT)δ(t−kT)이고, z-변환은 Z(f∗(t))=F(z)이다.
α,β는 상수이다.
상수 곱
Z(αf(t))=k=0∑∞αf(kT)δ(t−kT)=αk=0∑∞f(kT)δ(t−kT)=αZ(f(t))=aF(z)
선형성
f(t)=αx(t)+βg(t)z−transformF(z)=αX(z)+βG(z)
지수함수 곱
Z[e−atf(t)]=F(zeaT)
증명 :
Z[e−atf(t)]=k=0∑∞e−atf(kT)z−k=k=0∑∞f(kT)(zeaT)−k=F(zeaT)
이동
뒤로 이동(Backward shift)
Z[f(t−nT)]=z−nF(z)
증명 :
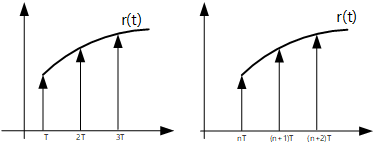
Z[f(t)]=f(0)+zf(T)+z2f(2T)+...
실시간 nT샘플이 뒤로 이동하면
Z[f(t−nT)]=znf(0)+zn+1f(T)+zn+2f(2T)+...=zn1(f(0)+zf(T)+z2f(2T)+...)=z−nF(z)
앞으로 이동(Forward shift)
Z[f(t+nT)]=znF(z)−znf(0)−zn−1f(T)−zn−2f(2T)−...−zf(n−1)
증명 :
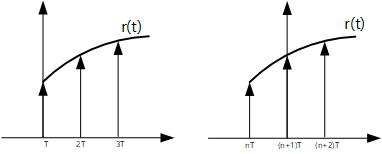
Z[f(t+T)]=f(T)+zf(2T)+z2f(3T)+...
z1Z[f(t+T)]=zf(T)+z2f(2T)+z3f(3T)+...
z1Z[f(t+T)]+f(0)=f(0)+zf(T)+z2f(2T)+z3f(3T)+...
z1Z[f(t+T)]+f(0)=F(z)
Z[f(t+T)]=zF(z)−zf(0)
비슷한 방법으로
Z[f(t+2T)]=zF(z+T)−zf(1)=z2F(z)−z2f(0)−zf(T)
초기값
f(0)=t→0limf(t)=z→∞limF(z)
증명 :
F(z)=f(0)+zf(T)+z2f(2T)+...
z→∞limF(z)=f(0)
최종값
f(∞)=t→∞limf(t)=z→1lim[(z−1)F(z)]
증명 :
Z[f(t)]=F(z)=k=0∑∞f(kT)z−k(1)
Z[f(k+T)]=zF(z)−zf(0)=k=0∑∞f(k+T)z−k(2)
식(1)에서 식(2)를 빼면 극한을 취한다.
z→1lim[(z−1)F(z)−zf(0)]=z→1lim[k=0∑∞f(k+T)z−k−k=0∑∞f(kT)z−k]=k=0∑∞z→1lim[(f(k+T)−f(k))z−k](3)
z→1lim[(z−1)F(z)−zf(0)]=f(∞)−f(0)(4)
z→1lim[(z−1)F(z)]=f(∞)(5)


로그인 하면 댓글을 쓸 수 있습니다.