강의노트 지상제어기 설계 - 예제
- 지상제어기 설계
지상제어기 설계
- 개루프 전달함수가 이다. 성능명세에서 속도오차상수는 20, 정정시간 1초이하 그리고 감쇠비는 0.707이다.
설계 )
1-1) 주어진 시스템의 근궤적을 그린다.
1-2) 근궤적에서 감쇄계수가 0.707일때의 이득을 찾는다.
근궤적에서 y축과의 각도가 $$\\sin \\theta = 0.707$$를 만족하는 점을 찾는다.
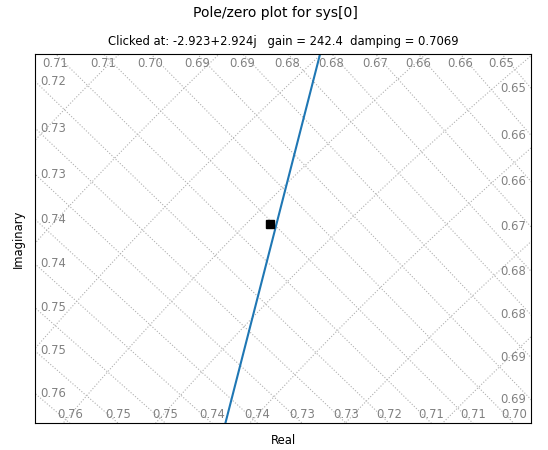
위 그림은 근궤적을 확대해서 damping값이 0.707이 되는 점을 찾는 것이다. 찾은 값은 242.4정도이다. 이 값이 $$K_u$$가 된다.
1-3) 이득을 위에서 얻은 값을 넣고 램프응답을 그려본다.
 응답 오차는 다음과 같다.
응답 오차는 다음과 같다.

1-4) 속도오차상수가 원하는 20일때의 응답을 확인해 본다.
이득이 2000이었을 때의 응답은 다음과 같다.

응답 오차는 다음과 같다.

위는 진동하는 형태가 된다.
1-5) 원하는 극점을 계산한다. a와 ts로 부터 를 구할 수 있다.
$$ \\omega = \\dfrac{3.2}{a \\times t_s}$$
$$\\omega$$와 $$a$$로부터 원하는 극점 $$p$$를 구할 수 있다.
$$p$$는 $$s^2 + 2a\\omega s + \\omega^2 = 0$$의 해이다.
1-6) 보상기는 원하는 극점의 실수값의 1/10에 해당하는 값을 b로 잡고 가 되게 값을 정한다.
그리고
즉, 보상기의 이득이 1이 되도록 만들어 준다.
보상기를 삽입한 후의 결과는 다음과 같다.
 오차 그래프는 다음과 같다.
오차 그래프는 다음과 같다.

보상전(검정색), 원하는 속도오차상수(파란색) 그리고 보상후(빨간색)의 오차 그래프는 다음과 같다.

- 보상전과 보상후의 제동비는 0.206으로 한다. 정상상태 오차가 보상전에 비해 10배로 줄이도록 제어기를 설계하여라.
설계) lag_02.py
시스템 G에 대한 근궤적을 그리고 제동비 0.206에 해당하는 각도에 해당하는 선을 근궤적위에 그린다. 근궤적과 선과의 교차점 과 이때의 이득 일때의 정상상태 오차를 계산한다.
이득 409일때의 시스템 응답은 다음과 같다. 정상상태 오차는 10%이다.

정상상태가 10배 줄이도록 를 계산한다.
위의 식에서 , 그러므로 가 된다.
점은 의 x축의 값의 0.1배 로 정했다. 로 정한다. 제어기는
제어기를 적용한 시스템 응답은 다음과 같다.

- 해바리기 시스템을 지상 제어기로 보상, 보상후 특성이 다음과 같도록 제어기를 설계하여라. 램프 입력에 대한 정상상태 오차 0.01이하, 최대 오버슛 5%이하, 정착 시간 0.5초 이하.
설계 lag_03.py)
오버슛으로부터 감쇄계수를 구한다.
감쇄계수와 정정시간으로부터 고유주파수를 구한다.
감쇄계수와 주파수로 원하는 시스템의 극점을 구한다.
플랜트의 근궤적과 원하는 시스템 극점을 같이 표시한 그래프다. 시스템의 원하는 극점의 원점에서의 연장선과 근궤적의 만나는 극점의 이득()가 된다.

보상전 시스템 응답

그리고 정상상태 오차가 0.01이 되도록 으로
이다.
원하는 극점의 실수 값보다 10배 작은 값으로 세팅한다.
는 로 설정한다.
지상제어기는 이 되고 이를 적용한 시스템의 응답은 다음과 같다.

보상 전과 보상 후의 오차 그래프는 다음과 같다.

- 안테나 위치 제어 시스템을 지상 제어기로 보상한다. 보상전보상후에는 최대 오버슛이 16%, 램프 입력에 대한 정상상태 오차는 보상전에 비해 10배 정도 줄이도록 제어기를 설계하여라.
로그인 하면 댓글을 쓸 수 있습니다.